Proper Trigonometry For Rotating A Point Around The Origin

Do either of the below approaches use the correct mathematics for rotating a point? If so, which one is correct?

POINT rotate_point(float cx,float cy,float angle,POINT p)
{
  float s = sin(angle);
  float c = cos(angle);

  // translate point back to origin:
  p.x -= cx;
  p.y -= cy;

  // Which One Is Correct:
  // This?
  float xnew = p.x * c - p.y *开发者_如何学运维 s;
  float ynew = p.x * s + p.y * c;
  // Or This?
  float xnew = p.x * c + p.y * s;
  float ynew = -p.x * s + p.y * c;

  // translate point back:
  p.x = xnew + cx;
  p.y = ynew + cy;
}

---

From Wikipedia

To carry out a rotation using matrices the point (x, y) to be rotated is written as a vector, then multiplied by a matrix calculated from the angle, θ, like so:

where (x′, y′) are the co-ordinates of the point after rotation, and the formulae for x′ and y′ can be seen to be

---

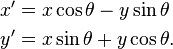
It depends on how you define angle. If it is measured counterclockwise (which is the mathematical convention) then the correct rotation is your first one:

// This?
float xnew = p.x * c - p.y * s;
float ynew = p.x * s + p.y * c;

But if it is measured clockwise, then the second is correct:

// Or This?
float xnew = p.x * c + p.y * s;
float ynew = -p.x * s + p.y * c;

---

This is extracted from my own vector library..

//----------------------------------------------------------------------------------
// Returns clockwise-rotated vector, using given angle and centered at vector
//----------------------------------------------------------------------------------
CVector2D   CVector2D::RotateVector(float fThetaRadian, const CVector2D& vector) const
{
    // Basically still similar operation with rotation on origin
    // except we treat given rotation center (vector) as our origin now
    float fNewX = this->X - vector.X;
    float fNewY = this->Y - vector.Y;

    CVector2D vectorRes(    cosf(fThetaRadian)* fNewX - sinf(fThetaRadian)* fNewY,
                            sinf(fThetaRadian)* fNewX + cosf(fThetaRadian)* fNewY);
    vectorRes += vector;
    return vectorRes;
}