目录
- 置信椭圆原理及椭圆图形绘制
- 置信椭圆长短轴计算
- 置信椭圆-python
- 总结
置信椭圆原理及椭圆图形绘制
置信椭圆长短轴计算

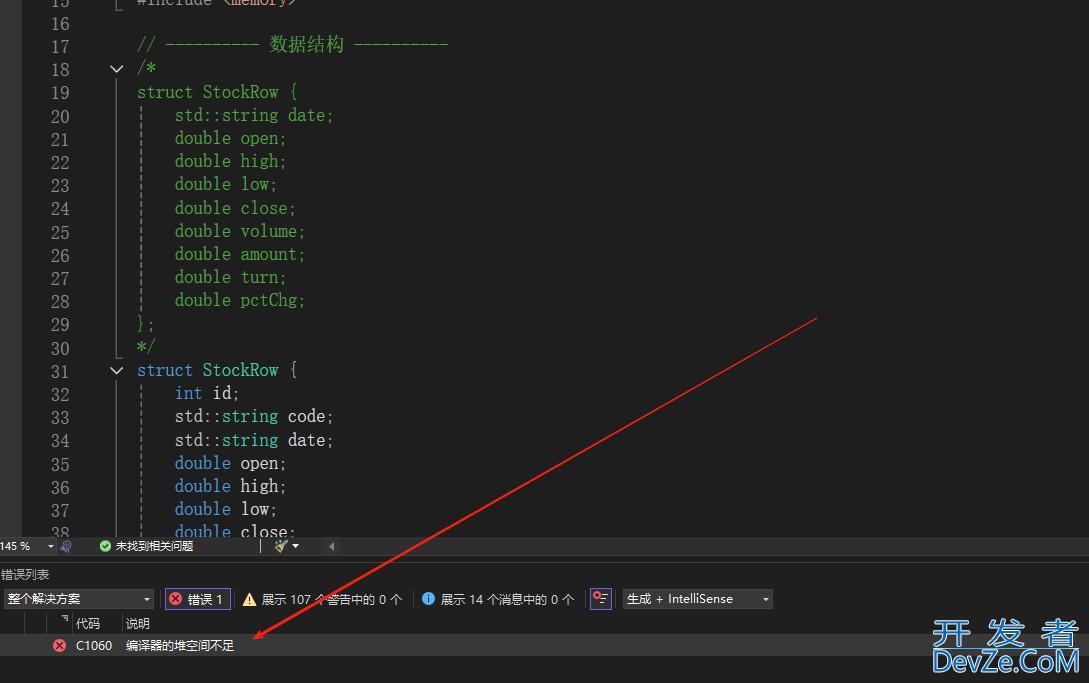
def confidence_oval(self,factor, ppf_rate):
pca1_std = np.std(factor.iloc[:, 0])
pca2_std = np.std(factor.iloc[:, 1])
f_value = scipy.stats.f.ppf(ppf_rate, dfn=2, dfd=factor.iloc[:, 0].shape[0] - 2)
x_axis = np.sqrt(
pca1_std ** 2 * f_value * 2 * ((factor.iloc[:, 0].shape[0] - 1) / (factor.iloc[:, 0].shape[0] - 2)))
y_axis = np.sqrt(
pca2_std ** 2 * f_value * 2 * ((factor.iloc[:, 0].shape[0] - http://www.devze.com1) / (factor.iloc[:, 0].shape[0] - 2)))
x_axis = '%.2f' % x_axis
y_axis = '%.2f' % y_axis
return x_axis, y_axis
Python图形绘制
def elli_plot(self,full_data, ellipse, y):
'''
:param full_data: pls后的点
:param ellipse: [椭圆长轴,椭圆短轴]
:param y:
:return:
'''
fig = plt.figure(figsize=(15, 5))
ax = fig.add_subplot(111)
elli = Ellipse(xy=(0, 0), width=float(ellipse[0]) * 2, height=float(ellipse[1]) * 2)
ax.add_patch(elli)
# 偏厚
outlier_data = y.loc[y[y.columns[0]] == 3, :]
# 偏薄
outlier_data_less = y.loc[y[y.columns[0]] == 1, :]
inner_data = full_data['pls']['pls'].loc[full_data['pls']['pls'].index.isin(outlier_data.index.tolist()+outlier_data_less.index.tolist(编程客栈)) == False, :]
ax.plot(outlier_data.iloc[:, 0], outlier_data.iloc[:, 1], 'ro')
ax.plot(outlier_data_less.iloc[:, 0], outlier_data_less.iloc[:, 1], 'bo')
ax.plot(inner_data.iloc[:开发者_C教程, 0], inner_data.iloc[:, 1], 'yo')
name = str(self.picture_id)
plt.savefig("E:\\shhl\\1118_两次PLS\\偏厚\\图\\"+name+".png")
self.picture_id = self.picture_id +1
plt.show()
from matplotlib.patches import Ellipse, Circle
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ell1 = Ellipse(xy = (0.0, 0.0), width = 4, height = 8, angle = 30.0, facecolor= 'yellow', alpha=0.3)
cir1 = Circle(xy = (0.0, 0.0), radius=2, alpha=0.5)
ax.add_patch(ell1)
ax.add_patch(cir1)
x, y = 0, 0
ax.scatter([0,1], [0,1],color='red')
ax.scatter([2,1], [1,1],color='green')
plt.axis('scaled')
plt.axis('equal') #changes limits of x or y axis so that equal increments of x and y have the same length
plt.show()
置信椭圆-python
卡方概率表:https://people.richland.edu/androidjames/lecture/m170/tbl-chi.html
opencv画椭圆:https://docs.opencv.org/2.4.9/modules/core/doc/drawing_functions.html?highlight=ellipse#cv2.ellipse
numpy.linalg.eig() 特征向量求解矩阵:https://docs.scipy.org/doc/numpy-1.10.1/reference/generated/numpy.linalg.eig.html
cov = phpnp.cov(x, y) #计算协方差矩阵 lambda_, v = np.linalg.eig(cov) # 计算矩阵特征向量 lambda_ = np.sqrt(lambda_) s=4.605 #根据置信区间查卡方概率表 95% 5.991 99% 9.21 90% 4.605 ax = plt.subplot(111, ASPect=‘equal') ell = Ellipse(xy=(np.mean(x), np.mean(y)), width=lambda_[0]*np.sqrt(s) *2, height=lambda_[1]*np.sqrt(s)*2, angle=np.rad2deg(np.arccos(v[0, 0])),facecolor=‘yellow',alpha=0.3) ax.add_artist(ell) plt.scatter(x, y) plt.axis(‘scaled') plt.axis(‘equal') plt.show()

总结
以上为个人经验,希望能给大家一个参考,也希望大家多多支持我们www.devze.com。


 加载中,请稍侯......
加载中,请稍侯......
精彩评论